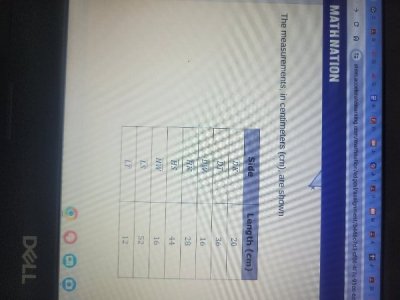
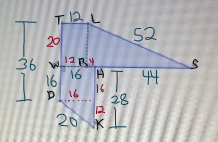
View attachment 997847 (blue numbers are from the chart, red are my additions)
I'm assuming here that the angles at R are right angles, and it's just too small to see the little symbol (but is does check out via Pythagorean Theorem with the sides of the triangle I end up getting, so I'm going with it for now.)
Step 1 - Since DT is 36 and DW is 16, WT is 20 (and so is RL).
Step 2 - If WH is 16 and WR is 12, then RH is 4, so the full length of the base of the big triangle (RS) is 48.
Step 3 - Complete the square by drawing a dotted line from D to HK, breaking the 28 into 16+12.
(I double-checked here that the small triangle "works" as a right triangle with 12,16,20 and so does the big one.)
Now you just have 4 separate shapes to calculate the areas of and add them together:
Upper left rectangle (length times width) = 12x20 =
240
Square (same formula) = 16x16 =
256
Small triangle (1/2 base times height) = (12x20)/2 =
120
Large triangle (same formula) = 48x20)/2 =
480
Final total area = 1,096 square centimeters.